채권 가격과 시장 금리의 관계
채권 가격 (bond price)과 시장 금리(yield rate, 채권 수익률)는 역의 관계(inverse relationship)
- 금리가 오르면 채권 가격은 하락하고,
- 금리가 내리면 채권 가격은 상승한다.
왜?
- 시장 금리가 상승하면 기존의 낮은 금리를 가진 채권의 상대적 매력이 떨어지므로 가격이 하락하고,
- 시장 금리가 하락하면 기존의 높은 금리를 가진 채권이 더 매력적으로 보이므로 가격이 상승한다.
채권의 현재 가치(PV)를 수식으로 표현하면 다음과 같다.
\[
P = \sum_{t=1}^{T} \frac{C}{(1 + r)^t} + \frac{F}{(1 + r)^T}
\]
여기서,
- \(P\) : 채권 가격 (Present Value)
- \(C\) : 매년 지급되는 쿠폰 이자 (Coupon Payment)
- \(F\) : 만기 시 원금(Face Value)
- \(r\) : 시장 금리 (Yield Rate)
- \(T\) : 잔존 만기
시장금리(\(r\))가 증가하면 할인율이 커져서 내가 가진 채권의 현재 가치(\(P\))가 낮아짐
예제 : 시장 금리 하락 시 채권 가격 변화
가정:
- 채권의 액면가: 1,000달러
- 쿠폰 이자율: 5% (연간)
- 만기: 3년
- 현재 시장 금리: 5% → 2% (3% 하락)
경기불황 때문에 기준금리가 내려가서 시장 금리가 하락하면,
새로 발행되는 2% 금리의 채권보다 기존 5%의 쿠폰을 지급하는 채권이 더 매력적으로 보이므로,
기존 채권의 가격이 상승한다.
Term (채권의 기간)
채권 금리는 단순히 하나의 고정된 값이 아니라, 만기에 따라 다르게 형성됨.
- 단기 채권(Short-term bonds, 1년 이하): 단기 금리는 중앙은행의 정책금리(예: 연준의 FFR, 한국은행의 기준금리)와 직접적으로 연결됨.
- 중기 채권(Mid-term bonds, 2~10년): 경제 성장률, 기대 인플레이션, 신용 위험 등에 영향을 받음.
- 장기 채권(Long-term bonds, 10년 이상): 장기 기대 인플레이션, 국가 신용, 경기 사이클 등에 따라 수익률이 결정됨.
Duration (채권 듀레이션)
채권은 듀레이션(Duration)이 길수록 금리 변화에 대한 가격 민감도가 커진다.
- 장기 채권: 금리 변화에 더 민감
- 단기 채권: 금리 변화에 덜 민감
Term Structure(기간구조)
Term Structure는 채권 시장에서 만기(term)에 따라 형성되는 금리 구조
Term Structure는 주로 Yield Curve(수익률 곡선)의 형태로 시각화된다.
채권 투자 전략
- 금리 상승 (Yield 상승) 예상 → 채권 가격 하락 → 기존 장기 채권 보유자는 손해. 기존 장기 채권을 매도하고, 새로운 금리가 반영된 채권을 매수. 기준금리 상승때문에 단기 채권은 괜찮음.
- 금리 하락 (Yield 하락) 에상 → 채권 가격 상승 → 기존 장기 채권 보유자는 이득. 기존 채권을 보유하여 가격 상승에 따른 자본 이득(capital gain) 확보. 장기 채권을 보유하는 것이 유리.
Yield Curve(수익률 곡선)
Yield Curve는 만기별 수익률을 연결한 곡선으로, 주요 형태는 3가지:
- 정상적인 형태(Normal Yield Curve): 장기 금리가 단기 금리보다 높음 → 경제 성장이 기대되는 경우
- 역전된 형태(Inverted Yield Curve): 장기 금리가 단기 금리보다 낮음 → 경기 침체 신호
- 평평한 형태(Flat Yield Curve): 단기와 장기 금리 차이가 거의 없음 → 경기 전환기
이렇게 다양한 형태가 나타나는 이유를 설명하는 이론들에는, 금리 기대이론(Expectations Hypothesis), 유동성 프리미엄 이론(Liquidity Premium Theory), 시장 분할 이론(Market Segmentation Theory) 등이 있음.
Yield Curve(수익률 곡선)는 본질적으로 \((\text{만기}, \text{yield})\) 쌍에 대한 Conditional Expectation Model을 적용한 결과라고 볼 수 있다.
채권 시장에서 다양한 만기의 국채(예: 1년, 2년, 5년, 10년, 30년 등)의 수익률 데이터를 수집하면, 기본적으로 (만기, yield) 쌍의 산점도(scatter plot)를 얻을 수 있다.
이후, Yield Curve는 이러한 데이터를 조건부 기대값 모형 (Conditional Expectation model)을 사용하여 스무딩(Smoothing)하거나 추정(Fitting)한 것이라고 볼 수 있다.
수익률 곡선을 추정하는 대표적인 방법으로 다음과 같은 모델들이 있다.
Spline Regression
- Cubic Spline 또는 B-spline을 사용하여 여러 구간에서 스무딩된 Yield Curve를 만듬.
Nelson-Siegel & Svensson model
Gaussian Process, Neural Networks
- Gaussian Process Regression (GPR) 또는 딥러닝 모델(Neural Networks)을 활용하여 Yield Curve를 추정하는 방법
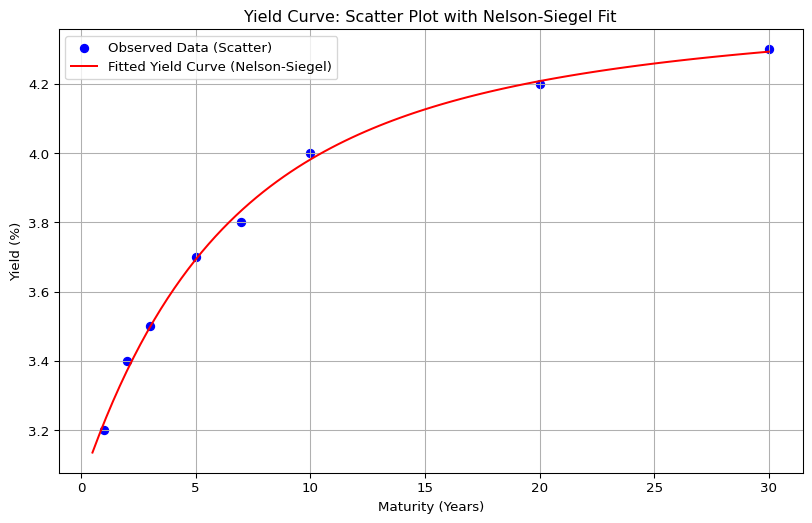
Code: Scatter Plot + Yield Curve
(만기, 수익률) 데이터 산점도를 그린 후, 스무딩된 Yield Curve를 적용.
Code
# Yield Curve(수익률 곡선)**는 본질적으로 (term,yield) 쌍에 대한 Conditional Expectation Model을 적용한 결과
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
# 예제 데이터 (만기, 수익률)
maturity = np.array([1, 2, 3, 5, 7, 10, 20, 30]) # 만기 (years)
yield_rates = np.array([3.2, 3.4, 3.5, 3.7, 3.8, 4.0, 4.2, 4.3]) # 수익률 (%)
# Nelson-Siegel 모델 함수 정의
def nelson_siegel(T, beta0, beta1, beta2, tau):
return beta0 + beta1 * (1 - np.exp(-T/tau)) / (T/tau) + beta2 * ((1 - np.exp(-T/tau)) / (T/tau) - np.exp(-T/tau))
# 초기값 설정 및 최적화
popt, _ = curve_fit(nelson_siegel, maturity, yield_rates, p0=[4, -1, 1, 2])
# 스무딩된 곡선 생성
T_fit = np.linspace(0.5, 30, 100) # 연속적인 만기 값
Y_fit = nelson_siegel(T_fit, *popt)
# 산점도 및 수익률 곡선 그래프
plt.figure(figsize=(10, 6))
plt.scatter(maturity, yield_rates, color='blue', label="Observed Data (Scatter)")
plt.plot(T_fit, Y_fit, color='red', linestyle='-', label="Fitted Yield Curve (Nelson-Siegel)")
plt.xlabel("Maturity (Years)")
plt.ylabel("Yield (%)")
plt.title("Yield Curve: Scatter Plot with Nelson-Siegel Fit")
plt.legend()
plt.grid(True)
plt.show()