05 Strategy

Author

gitSAM

Published

March 31, 2025

1 Motivation and Market Philosophy

Traditional asset pricing frameworks rest on no-arbitrage principles and risk-return tradeoffs, assuming that all assets exist to offer compensation for exposure to priced risks. Under such models, individual asset returns are interpreted as linear functions of sensitivities to systematic risk factors.

In contrast, the TBTF (Too Big To Fail) strategy is motivated by a fundamentally different view of financial markets under late-stage capitalism. We argue that the secondary stock market reflects persistent dominance by a small subset of firms whose market power is self-reinforcing. These firms attract new capital not due to risk-efficiency, but due to narrative-driven legitimacy and path-dependent concentration of initial endowment.

This motivates a strategy grounded not in diversification or risk exposure, but in capital persistence, market lock-in, and capital hierarchy.

2 Portfolio Selection Rule

The TBTF strategy is constructed under When-What–How framework:

  • When: look-back window (in-sample estimation) & look-forward window (rebalancing frequency)
  • What: asset universe (e.g. all US-listed stocks) & selection rule (e.g. top-n market cap)
  • How: asset weighting scheme (e.g. convex capital concentration fit)

2.1 Asset Universe

Our strategy operates on the full set of U.S. listed common stocks traded on NYSE, NASDAQ, and AMEX. Stocks with non-positive market capitalization are excluded to avoid bankrupt or illiquid firms.

Code 
import numpy as np
import pandas as pd
import sqlite3
con = sqlite3.connect(database="../../tbtf.sqlite")

crsp = pd.read_sql_query(
  sql="SELECT * FROM crsp",
  con=con,
  parse_dates={"date"}
)

2.2 Ranking and State Formation

Each month, firms are ranked by market capitalization. These rankings define discrete capital states (percentile bins). We focus on the top-decile (state = 10), selecting the top-\(n\) firms at time \(t\) based on market-cap rank. The baseline is \(n=10\), with robustness checks for \(n \in \{5, 7, 10, 15, 20\}\).

A Markovian state transition framework is imposed to capture the temporal dynamics of capital flow between ranked states. The top state exhibits persistent and asymmetric capital retention, supporting the capital lock-in hypothesis.

3 Asset Weighting Schemes

We evaluate several portfolio weighting methods:

  • TBTF (Convex Structural Weighting):
    Capital weights are determined by in-sample estimates of the convex relationship between market-cap rank and capital share. For example, specifications can be :

    • Quadratic Form: \(w_i \propto \alpha + \beta r_i + \gamma r_i^2\)
    • Exponential Form: \(w_i \propto \alpha e^{\beta r_i}\)
    • see Section 8 for more

    Note that the exponential form ensures structural monotonicity.

  • Value-Weighted (VW):
    Proportional to each firm’s market capitalization.

  • Equal-Weighted (EQ):
    Uniform allocation across all selected assets.

Code 
import matplotlib.pyplot as plt
import seaborn as sns

# 현재 경로 기준으로 상위 디렉토리로 경로 추가
import sys, os
sys.path.append(os.path.abspath('../..'))

import tbtf

To empirically validate the structural weighting functions, we fit several models to the in-sample relationship between rank and capital share. The following plots show the cross-sectional fitting results based on a representative rebalance date.

Code 
in_end = '2009-12-31'
in_sample_months = 48

print('Snapshot at:', in_end)
print('Look-back period:', in_sample_months, 'months')

df_in_sample, _ = tbtf.split_in_out_sample(crsp, in_end, in_sample_months)
Snapshot at: 2009-12-31
Look-back period: 48 months
Code 
fig, axes = plt.subplots(3, 2, figsize=(14, 15))
tbtf.plot_quadratic_fit(df_in_sample, n=10, state=10, ax=axes[0, 0])
tbtf.plot_exponential_fit(df_in_sample, n=10, state=10, ax=axes[0, 1])
tbtf.plot_mean_fit(df_in_sample, n=10, state=10, ax=axes[1, 0])
tbtf.plot_loess_fit(df_in_sample, n=10, state=10, ax=axes[1, 1])
tbtf.plot_bayes_fit(df_in_sample, n=10, state=10, ax=axes[2, 0])
tbtf.plot_spline_fit(df_in_sample, n=10, state=10, ax=axes[2, 1])
fig.suptitle(f"Fitted Capital Share Functions at {in_end}", fontsize=16)
plt.tight_layout()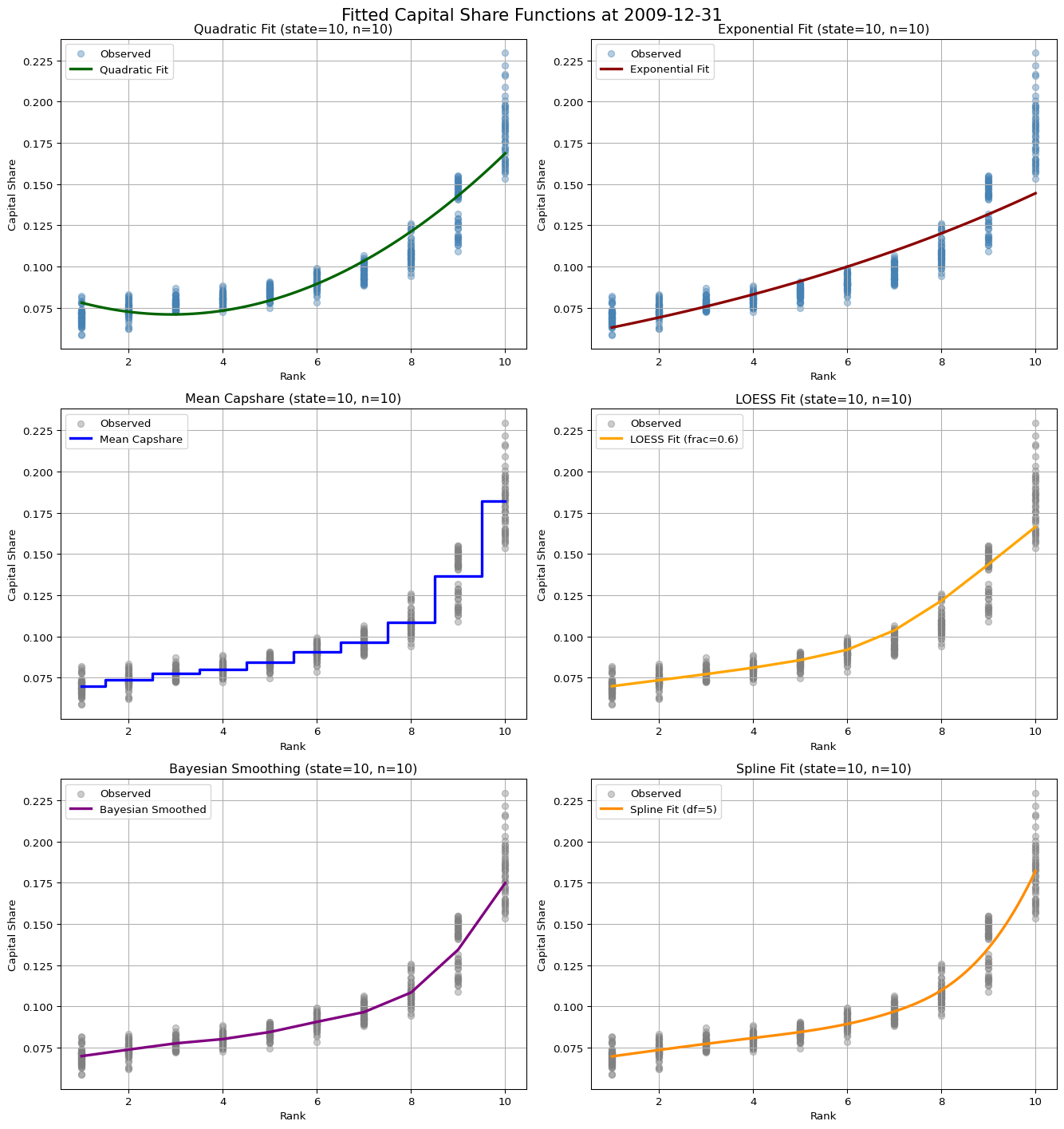

Empirical Fit at 2009-12-31
Code 
in_end = '2023-12-31'
in_sample_months = 48

print('Snapshot at:', in_end)
print('Look-back period:', in_sample_months, 'months')

df_in_sample, _ = tbtf.split_in_out_sample(crsp, in_end, in_sample_months)
Snapshot at: 2023-12-31
Look-back period: 48 months
Code 
fig, axes = plt.subplots(3, 2, figsize=(14, 15))
tbtf.plot_quadratic_fit(df_in_sample, n=10, state=10, ax=axes[0, 0])
tbtf.plot_exponential_fit(df_in_sample, n=10, state=10, ax=axes[0, 1])
tbtf.plot_mean_fit(df_in_sample, n=10, state=10, ax=axes[1, 0])
tbtf.plot_loess_fit(df_in_sample, n=10, state=10, ax=axes[1, 1])
tbtf.plot_bayes_fit(df_in_sample, n=10, state=10, ax=axes[2, 0])
tbtf.plot_spline_fit(df_in_sample, n=10, state=10, ax=axes[2, 1])
fig.suptitle(f"Fitted Capital Share Functions at {in_end}", fontsize=16)
plt.tight_layout()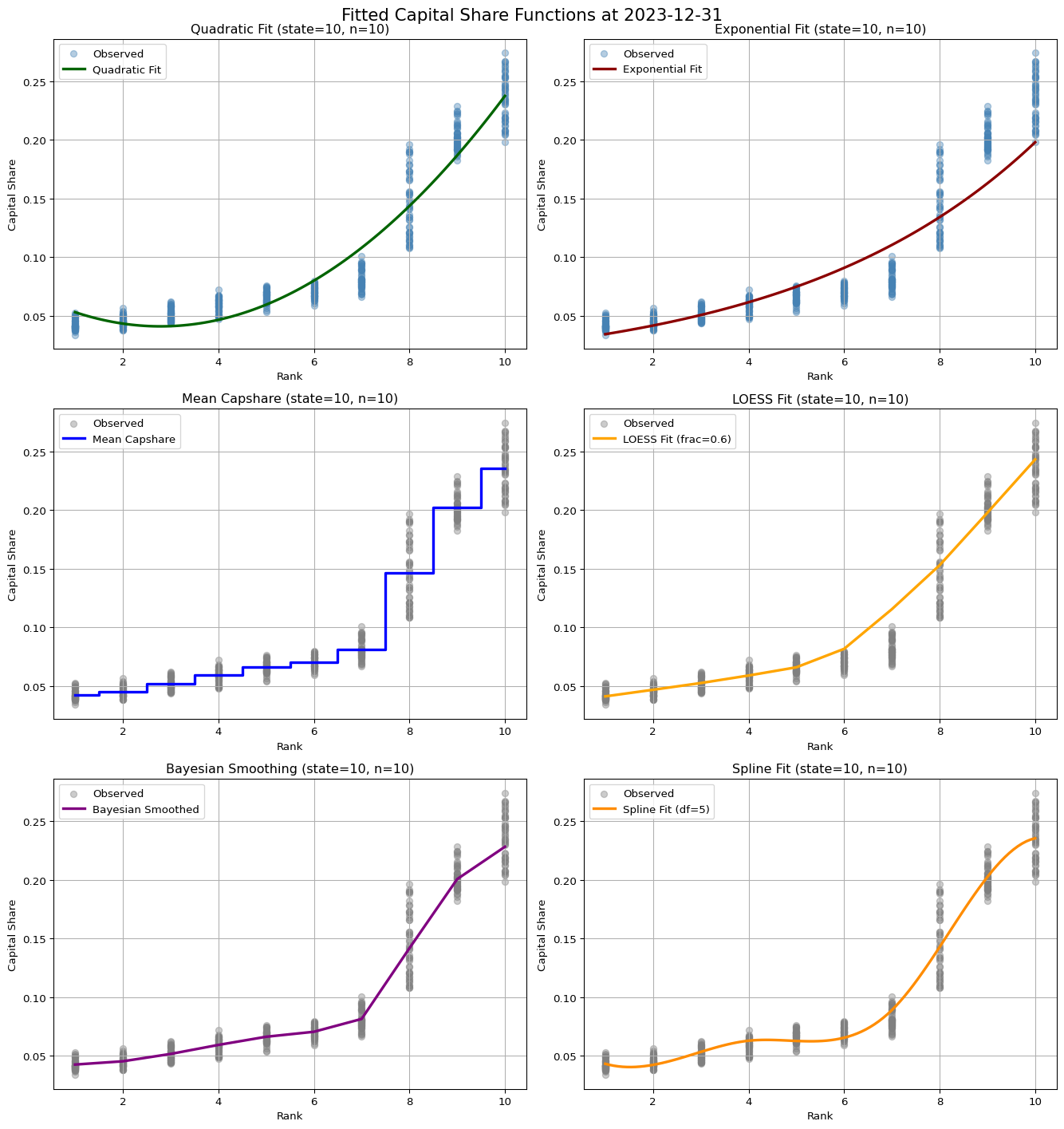

Empirical Fit at 2023-12-31

4 Rebalancing Frequency

We test fixed-interval rebalancing schemes:

  • Monthly (default)
  • Quarterly
  • Semiannual
  • Annual

Rebalancing frequency directly affects turnover and transaction cost implications. Monthly rebalancing is selected as the baseline to balance responsiveness with frictions.

5 Benchmark Portfolios

For external comparison, we use:

  • Pre-2010 Index Benchmarks: Dow Jones Industrial Average (^DJI), Nasdaq-100 (^NDX)
  • Post-2010 Index ETFs:
    • DIA (ETF version of DJIA, State Street Corporation ETF. Fund inception: 1998/01/14),
    • QQQ (ETF version of NDX. Nasdaq-100 ticker. the Invesco QQQ Trust. Fund inception: 1999/03/10),
    • SPY (The SPDR S&P 500 ETF, Fund inception: 1993/01/22),
    • VTI (Vanguard Total Stock Market ETF, Fund inception: 2001년 5월 24일),
  • Post-2010 Style Portfolios: Fama-French ME5 × PRIOR1/3/5, constructed with rolling monthly value- or equal-weighting

6 Strategic Rationale

The TBTF strategy is not merely a rule-based selection method. It reflects a structural argument that allocative efficiency in modern markets is compromised by persistent capital concentration. Instead of diversifying away idiosyncratic risk, markets are increasingly dominated by capital lock-in, hierarchy reinforcement, and narrative legitimacy.

This framework reconceptualizes the role of financial assets from carriers of risk to vehicles of structural dominance, and evaluates portfolio construction in light of this altered paradigm.

7 TBTF Strategy Pipeline

This appendix section outlines the modular structure of the TBTF portfolio strategy, from input specification to out-of-sample return generation and performance evaluation. The pipeline is designed to be flexible across different weighting schemes, rebalance frequencies, and strategy parameters.

7.1 Inputs (Arguments)

Argument Description
df Main input DataFrame (crsp) including fields such as date, permno, mktcap, ret, state, mktcap_lag, etc.
state_level Target capital state to define the asset universe, typically the top decile (e.g., 10).
top_n Number of assets to be selected at each rebalance point (e.g., n ∈ {5, 10, 20, 30, 50}).
rebalance_freq Rebalancing interval (e.g., '1M', '3M', '6M', '12M').
weighting_method One of 'equal', 'value', 'quadratic', or 'exponential'.
in_sample_period Estimation window for in-sample weight calibration (e.g., '2010-01-01' to '2013-12-31').
out_sample_period Evaluation window for out-of-sample backtesting (e.g., '2014-01-01' to '2023-12-31').
eta, p Parameters for CRRA utility (eta) and Omega ratio threshold (p).

7.2 Strategy Pipeline (Pseudo-code Logic)

7.2.1 Step 1: Data Partitioning & Filtering

in_sample = df[(df['date'] >= in_sample_start) & (df['date'] <= in_sample_end)]
out_sample = df[(df['date'] > in_sample_end) & (df['date'] <= out_sample_end)]
universe = df[df['state'] == state_level]
  • Restrict selection universe to target capital state (e.g., top decile).

7.2.2 Step 2: In-sample Weight Estimation

If weighting_method is 'quadratic' or 'exponential':

  • Estimate the relationship between within-state rank and capital share using in-sample data:

    • Quadratic:
      \[\text{CapShare}_i = \alpha + \beta \cdot \text{Rank}_i + \gamma \cdot \text{Rank}_i^2\]
    • Exponential:
      \[\text{CapShare}_i = \alpha \cdot e^{\beta \cdot \text{Rank}_i}\]

  • Save estimated coefficients:

    coefficients = {'alpha': ..., 'beta': ..., 'gamma': ...}

7.2.3 Step 3: Out-of-sample Portfolio Construction

For each rebalance date in the out-sample period:

  1. Filter to target state (state == state_level)
  2. Rank by market cap, select top n
  3. Assign weights:
    • Equal: \(w_i = 1/n\)
    • Value: \(w_i = \text{mktcap}_i / \sum \text{mktcap}\)
    • Quadratic: apply \(\hat{\alpha}, \hat{\beta}, \hat{\gamma}\) to rank
    • Exponential: apply \(\hat{\alpha}, \hat{\beta}\) to rank
  4. Store [date, permno, weight] for forward return application

7.2.4 Step 4: Portfolio Return Computation

At each evaluation date after rebalance:

  • Merge forward returns of selected assets
  • Compute portfolio return: \[R_t^{\text{portfolio}} = \sum_i w_{i,t} \cdot r_{i,t}\]
  • Construct time series of out-of-sample portfolio returns

7.2.5 Step 5: Turnover Calculation

For each rebalance window:

  • Calculate: \[\text{Turnover}_t = \sum_i |w_{i,t} - w_{i,t-1}|\]
  • Useful for assessing transaction costs and liquidity requirements

7.2.6 Step 6: Performance Evaluation

Using out-of-sample return series, compute:

  • Risk-Adjusted Metrics:

    • Sharpe ratio, Sortino ratio
    • Omega ratio (threshold = p)
    • Calmar ratio, maximum drawdown (MDD)
    • CRRA utility with risk aversion parameter eta

  • Return summary as dictionary:

    metrics_dict = {
    'Sharpe': ...,
    'Sortino': ...,
    'Omega': ...,
    'CRRA': ...,
    'CAGR': ...,
    'MDD': ...
}

7.3 Outputs

Output Description
returns_df Time series of out-of-sample portfolio returns
weights_df Portfolio composition (weights per date and permno)
turnover_df Time series of turnover at each rebalance point
metrics_dict Dictionary of strategy performance metrics

7.4 Module Lists

#| label: TBTF Strategy Full Module
#| warning: false
#| message: false

import pandas as pd
import numpy as np
import statsmodels.api as sm

# ----------------------------
# 1. Data Partitioning
# ----------------------------
def split_in_out_sample(df, in_end, in_sample_months=36, out_end=None):
    in_sample = df[(df['date'] <= in_end)].copy()
    if out_end:
        out_sample = df[(df['date'] > in_end) & (df['date'] <= out_end)].copy()
    else:
        out_sample = df[(df['date'] > in_end)].copy()
    return in_sample, out_sample

# ----------------------------
# 2. Weight Estimation
# ----------------------------
def estimate_exponential_weights(df_in_sample, n=10, state=10):
    # Placeholder for full implementation
    pass

def estimate_quadratic_weights(df_in_sample, n=10, state=10):
    # Placeholder for full implementation
    pass
# ----------------------------
# 3. Portfolio Construction
# ----------------------------
def construct_tbtf_exponential(crsp_df, target_state, top_n, params):
    # Placeholder for full implementation
    pass

def construct_tbtf_quadratic(crsp_df, target_state, top_n, params):
    # Placeholder for full implementation
    pass

# ----------------------------
# 4. Return and Turnover Calculation
# ----------------------------
def compute_return_tbtf(crsp, rebalance_dates, weighting_method='exponential', top_n=10, state=10, in_sample_months=36):
    # Placeholder for full implementation
    pass

def compute_return_pfo(crsp, rebalance_dates, weighting_method='vw', top_n=10):
    # Placeholder for traditional VW or EW method
    pass

def compute_turnover(weights_df, rebalance_dates):
    # Placeholder for full implementation
    pass

# ----------------------------
# 5. Performance Evaluation
# ----------------------------
def evaluate_performance(returns, eta=3, p=0.01, periods_per_year=12):
    # Placeholder for full implementation
    pass

# ----------------------------
# 6. Rebalance Date Utility
# ----------------------------
def get_rebalance_offset(rebalance_freq):
    # Placeholder for full implementation
    pass

# ----------------------------
# 7. Backtest Pipeline
# ----------------------------
def backtest_pipeline(crsp, in_end, out_end, in_sample_months, rebalance_freq, weighting_method, top_n, state, eta, p):
    # Placeholder for full backtest execution logic
    pass

# ----------------------------
# 8. Visualization (optional)
# ----------------------------
def plot_quadratic_fit(df_in_sample, n=10, state=10):
    # Placeholder for plot generation
    pass

def plot_exponential_fit(df_in_sample, n=10, state=10):
    # Placeholder for plot generation
    pass

8 Appendix: Alternative Fitting Methods for Capital Share Functions

Method Functional Form Statistical Interpretation Flexibility Stability Interpretability Complexity
Mean-Based Stepwise function Group-wise Sample Mean Low Low High Very Low
LOESS Local smoothing Nonparametric Local Regression Very High Medium Medium Moderate
Bayesian Global shrinkage estimator Hierarchical Bayesian Model Medium High Medium Moderate–High
Spline Smooth piecewise polynomial Semi-parametric Regression High Medium Medium Moderate

8.1 Mean-Based Estimation (1st Moment per Rank)

Definition
For each rank \(r \in \{1,\dots,10\}\), we estimate the average capital share over the in-sample period: \[ \hat{w}_r = \frac{1}{T} \sum_{t=1}^{T} w_{r,t} \]

Statistical Structure

  • A fully nonparametric approach, treating each rank as a discrete category.
  • Equivalent to a fixed effect model without regressors, estimating the group-wise sample mean.

Theoretical Interpretation

  • This is a form of empirical histogram fitting, relying only on the sample mean of observed capital shares.
  • The method does not require distributional assumptions and treats the sample average as representative, regardless of time variation or non-stationarity.

Advantages

  • Simple, intuitive, and computationally efficient.
  • Highly flexible due to the absence of structural assumptions.

Limitations

  • Very sensitive to variance and outliers in the capital share distribution at each rank.
  • No extrapolation or smoothing is applied across ranks.

8.2 LOESS (Locally Weighted Scatterplot Smoothing)

Definition
Capital share is estimated via local regression, using a kernel-weighted average of nearby observations: \[ \hat{w}_r = \sum_{j} K\left(\frac{r - j}{h}\right) w_j \] - \(K(\cdot)\) is a kernel function (e.g., tricube); \(h\) controls the bandwidth and smoothness.

Statistical Structure

  • A classic nonparametric regression method.
  • LOESS typically uses local polynomial regressions (order 0, 1, or 2) for smoothing.

Theoretical Interpretation

  • Constructs the overall rank–capshare curve as a composition of local approximations, rather than a single global function.
  • Highly sensitive to the bias-variance tradeoff depending on bandwidth \(h\).

Advantages

  • Effectively captures local irregularities in the rank–capshare mapping.
  • Very flexible, with no functional form assumptions.

Limitations

  • Poor extrapolation performance at boundary ranks (e.g., rank 1 and 10).
  • Bandwidth selection has a significant effect on smoothing behavior.

8.3 Bayesian Smoothing (Hierarchical Empirical Bayes)

Definition
Each rank-specific capital share \(w_r\) is modeled as a noisy observation from a latent distribution: \[ w_r \sim \mathcal{N}(\theta_r, \sigma_r^2), \quad \theta_r \sim \mathcal{N}(\mu, \tau^2) \]

Statistical Structure

  • A hierarchical Bayesian model that allows ranks to share strength through a common prior.
  • In the empirical Bayes setting, the hyperparameters \((\mu, \tau^2)\) are estimated from data.

Theoretical Interpretation

  • Stabilizes estimates for ranks with high variance by shrinking them toward the global prior.
  • Ranks near the center are barely adjusted, while outlier ranks are pulled closer to the mean.

Advantages

  • Produces stable estimates even under noisy or volatile capital share data.
  • Allows for uncertainty quantification via posterior distributions.

Limitations

  • Sensitive to prior or hyperparameter specification.
  • Implementation can be more complex than standard nonparametric methods.

8.4 Spline Smoothing (Piecewise Polynomial with Smooth Joints)

Definition
The rank–capshare function is approximated as a linear combination of spline basis functions: \[ \hat{w}_r = \sum_{k} \beta_k B_k(r) \] - \(B_k(r)\) are spline basis functions (e.g., B-splines or natural splines).

Statistical Structure

  • A semi-parametric regression approach.
  • The model is similar to linear regression but extended via basis transformation.

Theoretical Interpretation

  • Balances global fitting and local flexibility by using piecewise polynomial segments with smooth joints.
  • The number and placement of knots (and the degree of polynomials) determine flexibility.

Advantages

  • Produces smooth and differentiable fits across the rank domain.
  • Extrapolation is partially feasible, especially when using natural splines.

Limitations

  • Performance is highly dependent on the selection of knots.
  • Can overfit if too many basis functions are used.